NFA的最小化
约 1148 字大约 4 分钟
2024-12-28
Hopcroft’s algorithm
上一小节描述了如何将NFA转换为DFA。但是DFA的状态数量可能会非常多,这会导致程序的复杂度增加。因此我们需要对DFA进行最小化。最小化的目的是减少DFA的状态数量,同时保持DFA的功能不变。
最小化DFA采用的方法Hopcroft’s algorithm,他的主要思路是将DFA的状态进行划分,即 P=P1,P2,P3,...Pm包含了所有的DFA状态,其中每个 Pi 都包含了等价的DFA状态。更正式地来描述,它构建一个具有最少数量集合的划分,同时需满足以下两条规则::
- 对于 ∀c∈∑,如果 di,dj∈Ps;di→cdx;dj→cdy 并且此时 dx∈Pt,dy∈Pt。
- 如果 di,dj∈Pk,那么 di∈DA,dj∈DA。
规则一规定,同一集合中的两个状态对于每一个字符 c∈∑,必须转换到属于划分中单一集合的状态。规则二,规定任何一个单一集合要么包含接受状态,要么包含非接受状态,但不能同时包含两者。
我们现在对上面得到的DFA进行最小化。
- 初始化分割状态 P0={S1,S2,S3},P1={S0}。
- 处理 P0。经历字符 a,b,c 后,得到的状态分别是 {S1,S2,S3} 属于 P0 的子集,不存在多个状态集合,不分割。
- 处理 P1。经历字符 a,b,c 后,得到的状态分别是 {S1,S2,S3} 也属于 P0 的子集,不分割。
因此处理完之后,对状态重新计数,得到的最小DFA如下。 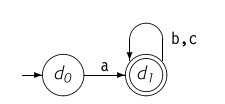
Brzozowski algorithm
下面介绍另一种DFA最小化的算法。Brzozowski algorithm。
子集构造方法通过系统地消除 ε 转移,并且合并NFA转换图中的路径,从而将NFA转换为DFA。 如果我们对某个前缀从开始状态有多条路径的NFA应用子集构造方法,这种方法会把这些路径合并成一条路径。由此产生的DFA不会有重复的前缀。因此我们可以从NFA直接得到最小化DFA,可以通过DFA来最小化DFA。
对于该算法,我们映入三个函数,其中 n 代表一个NFA:
reverse(n)。表示通过逆转所有转换的方向,把起始状态变为终止状态,并且添加一个新的初始状态,并将其连接到所有原本是接受状态的状态reachable(n)。返回DFA初始状态开始可以到达的所有状态和转换的集合。subset(n)。通过应用子集构造所确定的DFA。
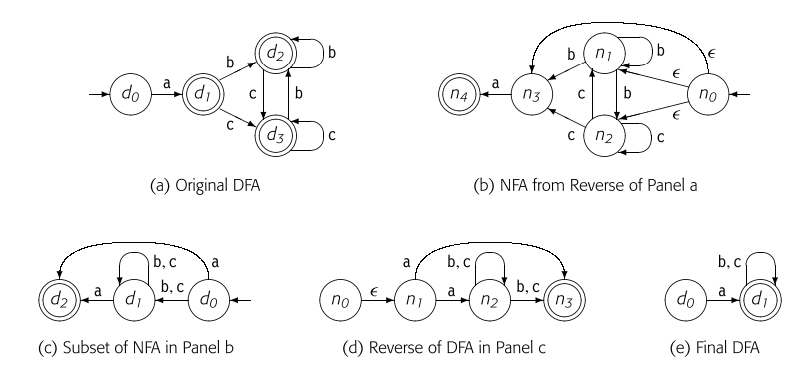 对这个DFA应用反转操作产生了图(b)中所示的NFA。接下来,算法将子集构造应用于这个NFA,以产生图(c)中所示的DFA。对图(c)应用反转操作得到图(d)中的NFA。将子集构造应用于这个NFA,产生了最终的、最小化的DFA,如图(e)所示。请注意,在这个例子中,reachable没有起到作用。
对这个DFA应用反转操作产生了图(b)中所示的NFA。接下来,算法将子集构造应用于这个NFA,以产生图(c)中所示的DFA。对图(c)应用反转操作得到图(d)中的NFA。将子集构造应用于这个NFA,产生了最终的、最小化的DFA,如图(e)所示。请注意,在这个例子中,reachable没有起到作用。
通过以上的描述,给定一个NFA n,那么最小化的等价DFA为:
reachable(subset(reverse(reachable(subset(reverse(n))))))
两者比较
Brzozowski算法可能会因为子集构造过程中可能构建出呈指数级增长的状态集合而变得昂贵。
Hopcroft算法具有更低的渐近复杂度:O(nlogn),其中 n 是输入有限自动机(FA)中的状态数。
两种算法之间的权衡并不是直截了当的。对各种FA最小化技术运行时间的研究表明,实际的运行时间取决于FA的具体属性。实际上,Brzozowski算法表现得相当不错。此外,Brzozowski算法的实现几乎肯定会比Hopcroft算法更简单。由于Brzozowski算法产生的是DFA,它可以被直接应用于Thompson构造的输出,从而省去了额外的一次子集构造应用。
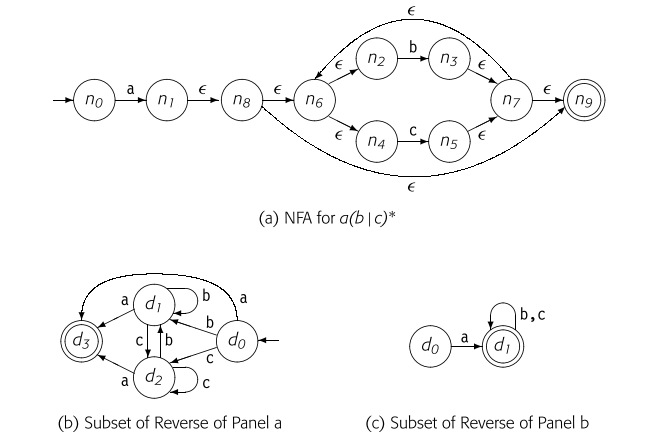
该图显示了该算法直接应用于Thompson构造为表达式 (b∣c)∗ 构建的NFA时所采取的步骤。图(a)显示了原始的NFA。图(b)显示了通过应用反转和子集构造转换后得到的DFA。图(c)显示了最终的DFA。。