这一节主要讲的是如何识别单词。一个逐字识别单词的算法简单且易于理解。扫描器会对每个字符进行一次测试，来判断是否符合单词。

假设存在一个名为 NextChar() 的函数，该例程返回连续的字符。代码依次测试字符 n、e 和 w。在每一步中，如果未能匹配到相应的字符，代码会拒绝该字符串并尝试其他操作。如果程序的唯一目的是识别“new”，那么在这种情况下它应该报告一个错误。但由于扫描器很少只识别一个单词，因此我们目前将这个错误路径故意模糊处理。因此我们很容易给出伪代码：

c = NextChar();
if( c == 'n') then
  c = NextChar();
  if( c == 'e') then
    c = NextChar();
    if( c == 'w')then
      report success;
    else
      try something else;
  else
    try something else;
else
  try something else;

并且可以给出其状态图:

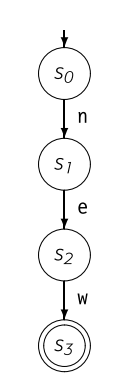
因此由状态图引入了形式化语言识别。状态转换图是代码实现的抽象表达，也可被视为正式的数学对象，称为有限自动机 Finite automata。后文简称FA。正式的FA定义是一个五元组包含 $(S,\sum,\delta,s_0,S_A)$。其中

• $S$ 代表了识别器的有限集合，包含错误状态 $s_e$。
• $\sum$ 代表了识别的有限的字母表，就是相当于状态转移图中边的标签的集合。
• $\delta$ 代表了识别器的状态转移函数。他将每个状态 $s \in S$ 对于每个字母 $c \in \sum$ 映射到下一个状态。即FA进行如下的转换 $s_{i} \xrightarrow{c} \delta\left(s_{i}, c\right)$
• $s_0$ 代表了设计的初始状态。
• $S_A$ 代表了可接受的状态，$S_A \subseteq S$。可接受状态在状态转移图中，用双圈进行表示。

更正式的说，如果字符串由 $x_1,x_2,x_3 ... x_n$ 组成。对于一个FA来说，能接受该字符串，当前仅当

$$\delta\left(\delta\left(\ldots \delta\left(\delta\left(\delta\left(s_{0}, x_{1}\right), x_{2}\right), x_{3}\right) \ldots, \mathrm{x}_{n-1}\right), x_{n}\right) \in S_{A}$$

更新日志

2024/12/26 12:27

查看所有更新日志

• ab405-更新了扫描器前两小节的内容于 2024/12/26