NFA

我们使用有限自动机工作的目标是自动化从一组正则表达式推导出扫描器的过程。本节开发了将正则表达式转换为有限自动机的构造方法。这些构造方法依赖于非确定性有限自动机（NFA）和确定性有限自动机（DFA）。可以从任何有限自动机构建一个正则表达式。这些构造方法共同形成一个循环，如图所示。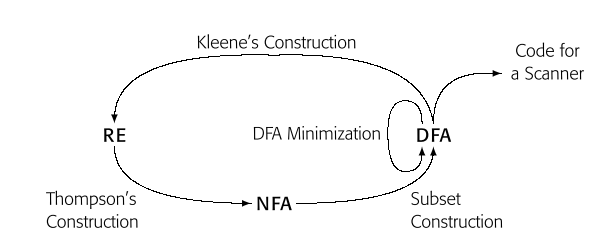

构造方法的循环证明了正则表达式和有限自动机具有等价的表达能力。也就是说，正则表达式可以表示任何可以用有限自动机识别的语言，并且有限自动机可以识别任何可以用正则表达式指定的语言。

NFA和DFA的区别

• NFA引入了空边 $\varepsilon$,并且NFA可能对一个字符产生两个状态转移，不能确定。
• DFA没用空边 $\varepsilon$,并且对于每一个字符都能产生确定的状态转移。

简而言之，就是DFA状态转移没有二义性，而NFA具有多重歧义。 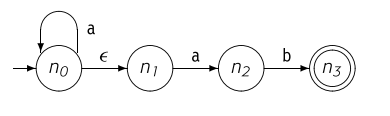对于上面的示例图，假设我们现在从状态 $n_0$ 开始如果下一个字符是 $a$，我们是选择 $n_0$ 的自循环的这条边，还是选择通过空边 $\varepsilon$ 到到达 $n_1$，再通过 $a$ 到达状态 $n_2$。这就是NFA的不确定性。

但是要强调的是NFA和DFA是等价的。

程序假如识别DFA的时候，会采取如下的措施：

• 每次NFA必须做出非确定性选择时，如果存在这样的转换，它会遵循导致接受状态的转换来处理输入字符串。这种使用全知NFA的模型吸引人之处在于它（表面上）保持了DFA明确的接受机制。本质上，NFA在每个点上猜测正确的转换。本质上是赌神。
• 每次NFA必须做出非确定性选择时，NFA会自我复制以追踪每一个可能的转换。因此，对于给定的输入字符，NFA及其复制品处于某个状态集合中。在这个模型中，NFA并发地追踪所有路径。这种的缺点是需要消耗大量内存。

NFA的构造

我们可以从正则表达式中构造NFA，对于前一节提到了正则表达式式的三个操作来说，我们有如下的构造法。称为Thompson's construction。 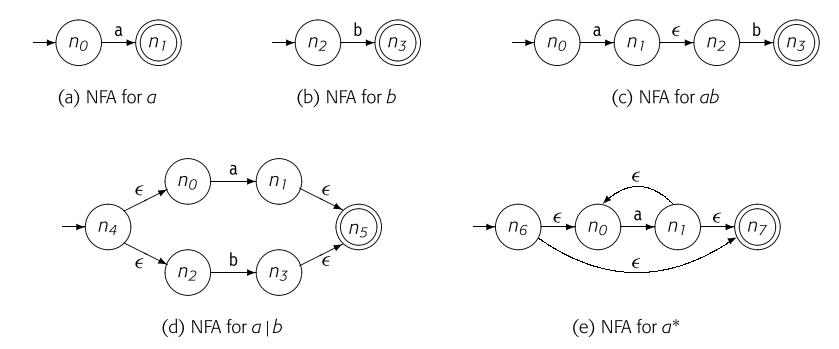以构造 $a(b|c)^*$ 的正则表达式为例。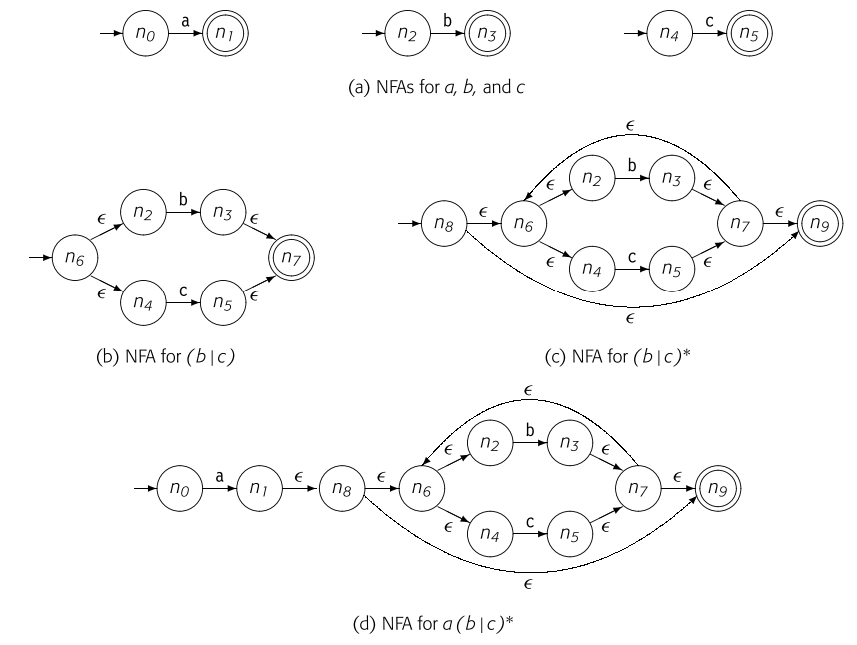

1. 构造 $a,b,c$ 的NFA。
2. 按照Thompson's construction，构造 $(b|c)$ 的NFA。
3. 按照Thompson's construction，构造 $(b|c)^*$ 的NFA。
4. 按照Thompson's construction，构造 $a(b|c)^*$ 的NFA。

这样按照Thompson's construction进行构造的好处是仅一个接受状态，它没有向外的转换。一个接受状态使得所有成功的匹配都指向同一个终点，这减少了复杂性，也避免了不必要的状态转换计算。也方便后续NFA到DFA的转换。

更新日志

2024/12/28 13:06

查看所有更新日志

• 4e0c4-更新完编译器扫描器于 2024/12/28