从DFA到正则表达式

我们在之前的NFA一节，引入了一张图。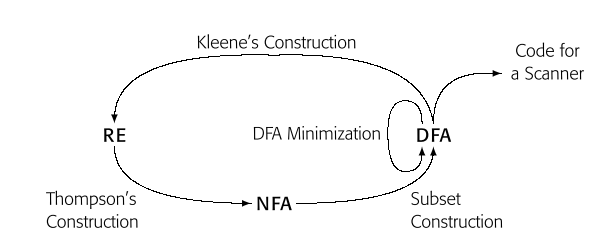

图中的Tompson's construction，Subset construction和DFA Minimization都在前面的章节中聊过了，还剩下从DFA到RE之间的Kleen's construction。

算法假设DFA的状态编号从 $0$ 到 $|D|-1$，DFA的接受状态集合为 $D_A$。

我们将符号 $R_{ij}^k$ 来表示描述所有从 $d_i$ 到 $d_j$的路径上而不经过编号高于$d_k$ 的状态的正则表达式。这里"通过"的意思是，从 $d_i$ 到 $d_j$ 之间的路径上，任何状态的编号都小于等于 $d_k$。假设一个DFA具有一个状态转移 $d_{1} {\rightarrow} d_{1 6}$,$R_{1,16}^2$ 将不会为空。

Kleen's construction的执行过程大概如下：

1. 初始化，算法将所有从 $d_i$ 到 $d_j$ 的直接路径，记作 $R_{ij}^{-1}$。当 $i = j$ 时，$R_{ij}^{-1}$ 为 $\varepsilon$。
2. 进行迭代，每次迭代都会构建更长的路径。每次通过添加通过 $d_k$的路径，利用 $R_{ij}^{k-1}$ 来计算 $R_{ij}^k$。
   • 从 $d_i$ 到 $d_k$ 的所有路径的集合，这些路径不经过编号高于k-1的状态，与 $d_k$到自身的任意路径相连接，这些路径也不经过编号高于 $k-1$ 的状态，再与从 $d_k$ 到 $d_j$ 的所有路径的集合相连接，这些路径同样不经过编号高于k-1的状态.

   • $$R_{i j}^{k} \gets R_{i k}^{k-1} \ ( R_{k k}^{k-1} )^{*} R_{k j}^{k-1} \ +R_{i j}^{k-1}$$

3. 当 $k$ 循环终止时，不同的 $R_{ij}^k$ 计算了图中所有的路径。
4. 此时从所有路径中，找到从起始状态 $d_0$ 到接受状态 $d_j \in D_A$ 的路径，这些路径构成了DFA的正则表达式。

更新日志

2025/1/4 14:08

查看所有更新日志

• a564f-寒假每日一题更新于 2025/1/4