NFA到DFA的转换

上一小节描述了NFA的构造方法，本节介绍如何将NFA转换为DFA。对于程序来说DFA的执行相对于NFA来说更容易模拟。因此构从正则表达式构造识别器的下一步是将NFA转换为等价的DFA。从NFA转换为DFA的转换方法被称为subset construction子集构造法。

• $\varepsilon-closure$ $\varepsilon$-闭包，对于给定的NFA状态集合，$\varepsilon-closure$ 是该集合中所有状态的集合，以及从该集合中的任何状态可以通过 $\varepsilon$ 转换到达的任何状态。
• NFA的初始状态的 $\varepsilon-closure$ 是DFA的初始状态。
• 针对每个DFA状态，对于NFA状态子集S，求输入每个字符 $c$ 后能到达的NFA状态的 $\varepsilon-$ 闭包并集 $\varepsilon-clousure(\delta(S,c))$。该集合对应于DFA中一个已有状态，或者是一个要新加的是DFA状态。下文用 $FollowEpsilon(\delta(S,c))$ 来表示这个并集。

我们拿下图进行举例说明。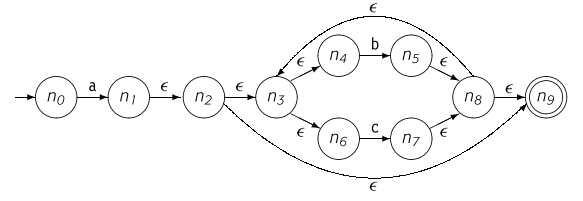

• 对于初始状态 $n_0$,记作 $d_0$。遍历字符a的 $\varepsilon-closure$ 是 $n_1,n_2,n_3,n_4,n_6,n_9$。记作 $d_1$。
• 将 $d_1$ 重复进行上次操作。遍历字符b边得到 $n_5,n_8，n_9,n_3,n_4,n_9$记作$d_2$，遍历字符c得到 $n_7,n_8,n_9,n_3,n_4,n_6$记作$d_3$。
• 重复上述操作，发现没有得到新的状态。操作结束，得到的DFA如下。

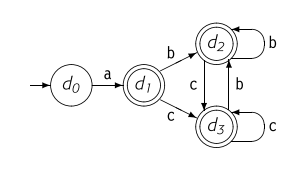
补充

子集构造是不动点计算的一个例子，这是一种特定的计算风格，在计算机科学的许多领域中经常出现。这类计算的特点是对来自一个已知结构域的一些集合反复应用单调函数。当计算达到进一步迭代不会产生新结果的状态时，即在相继迭代的空间中达到“不动点”时，这些计算就会终止。不动点计算在编译器构造中扮演着重要且反复出现的角色。

不动点算法的终止论证通常依赖于域的已知属性。对于子集构造而言，域 $D$ 是 $N$ 的子集的集合。该构造逐步建立集合 $Q$，其中每个 $q \in Q$ 是 $N$ 的一个子集。由于 $N$ 是有限的，因此其幂集 $2^N$ 也是有限的，这也就意味着 $Q$ 中的不同元素数量是有限的。

更新日志

2024/12/28 13:06

查看所有更新日志

• 4e0c4-更新完编译器扫描器于 2024/12/28