要构建一个令人满意的解析器，编译器编写者必须理解语法和解析器工程的基础知识。有了可用的解析器后，通常有办法可以提升其性能。本节将审视解析器构建中的两个具体问题。首先，我们考察对语法的转换，这些转换能够减少推导的长度，从而产生更快的解析过程。这些想法既适用于自上而下的解析器，也适用于自下而上的解析器。其次，我们讨论对语法以及动作（Action）和转义（Goto）表的转换，这些转换能够减小表的大小。这些技术仅适用于LR解析器。

自上而下和自下而上的解析器都会构建推导。对于推导中的每一个产生式，自上而下的解析器执行一次展开操作，而自下而上的解析器则执行一次归约操作。一个能够产生较短推导的语法，在解析时会花费较少的时间。

再次考虑经典的左递归表达式语法，如下图(a)所示。它的LR(1)表出现在图3.33中。即使对于简单的表达式，这个语法也会产生相当大的解析树。例如，a + 2 * b的解析树有14个节点，如下图(b)所示。其中五个节点是无法消除的叶节点；改变语法不能缩短输入程序。然而，内部节点的数量和位置则完全取决于推导过程。

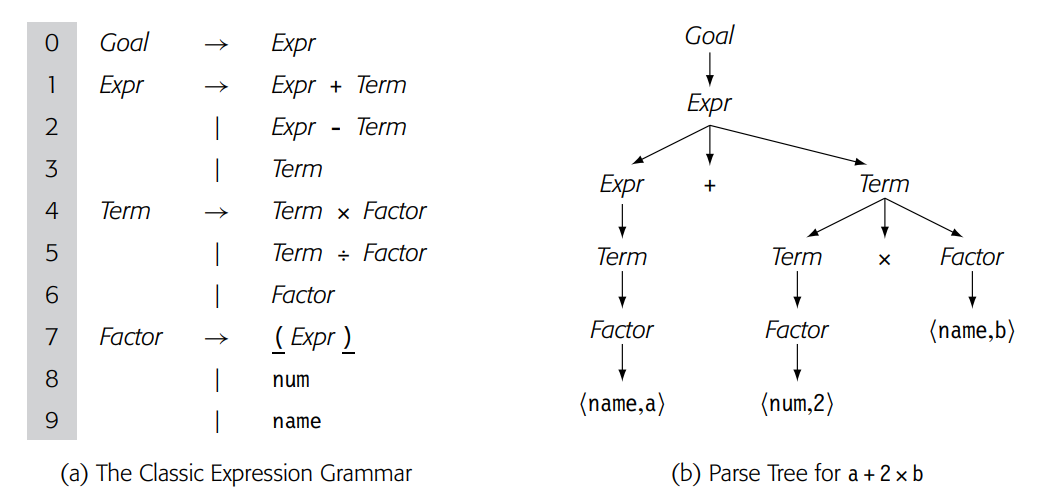
任何只有一个子节点的内部节点都是优化的候选对象。节点序列Expr→Term→Factor→>(name, a)使用了四个节点来表示输入流中的一个单词。我们可以通过将Factor的不同展开选项合并到Term中，从而消除至少一层，即Factor节点层，如下图 所示。这样做虽然使Term的选择数量增加了三倍，但却缩小了解析树的一层，如图2(b)所示。解析树的节点由原来的14减少到现在的11个。

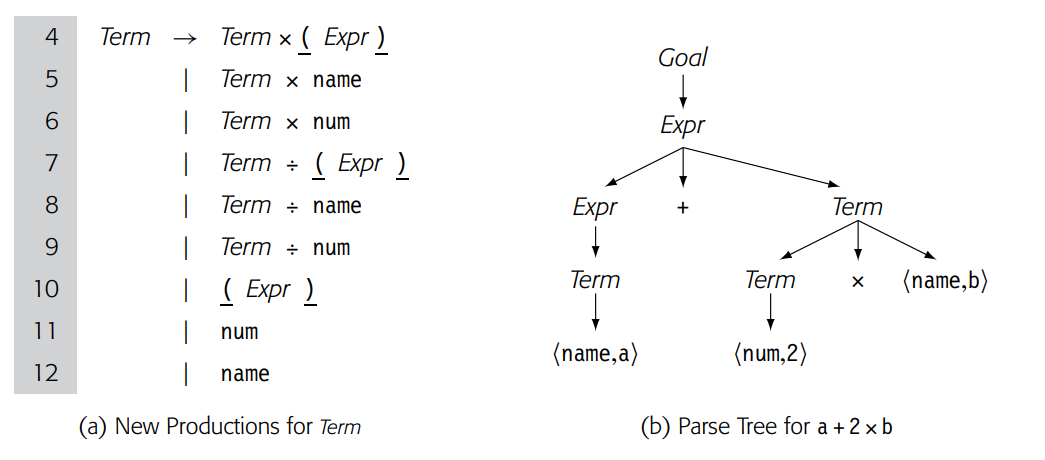
在LR(1)解析器中，这一改动消除了九个归约动作中的三个，并保持五个移进（shift）操作不变。在一个等价预测语法的自上而下的递归下降解析器中，它会消除14个过程调用中的3个。

一般来说，任何具有单个符号右侧的产生式都可以被合并。我们称这样的产生式为无用产生式。有时，无用产生式有助于使语法更紧凑，或许更易读，或迫使推导呈现出特定的形式。（回想一下我们最简单的表达式语法接受a + 2 * b但不会在解析树中编码任何优先级概念。）

无用产生式示例

考虑经典的左递归表达式语法：

Expr → Expr + Term | Term
Term → Term * Factor | Factor
Factor → (Expr) | name | number

在这个语法中，Factor的产生式右侧都只有一个符号。我们可以将Factor的产生式合并到Term中：

Term → Term * (Expr) | Term * name | Term * number 
Term → Term /(Expr) | Term /name |Term / number
Term → (Expr) | name | number

通过这种合并，我们消除了Factor这一层，将解析树的节点从14个减少到11个。在LR(1)解析器中，这消除了9个归约动作中的3个，同时保持5个移进操作不变。在递归下降解析器中，它消除了14个过程调用中的3个。

这种优化虽然增加了Term的产生式数量，但简化了解析树结构，提高了解析效率。无用产生式有时有助于使语法更紧凑和易读，但合并它们可以带来性能上的提升。

重要

消除无用产生式也有其代价。在LR(1)解析器中，这可能会使表更大。在我们的例子中，消除Factor从Goto表中去除了一个列，但是Term的额外产生式使CC的大小从32个集合增加到了46个集合。因此，表少了一列，但多了14行。最终的解析器执行的归约更少（运行更快），但表更大了。这里并没有列出。

减少LR(1)表的大小

不幸的是，即使是小型语法生成的LR(1)表也可能很大。 本节将描述其中的三种方法，它们都可以减少表的大小。

1. 缩减语法

   • 编译器编写者常常可以通过重新编码语法来减少产生式的数量。较少的产生式通常会导致较小的表。例如，在经典表达式语法中，数字和标识符之间的区别对于Goal、Expr、Term和Factor的产生式来说是无关紧要的。
   • 将两个产生式 Factor → num 和 Factor → name 替换为一个产生式 Factor → val 可以使语法缩小一个产生式。在Action表中，每个终结符符号都有其自己的列。将num和name合并成一个符号val会移除这些列中的一个。当然，扫描器（scanner）必须对num和name返回相同的句法类别或单词。
   • 类似的论点也适用于将乘法和除法运算符合并为一个终结符muldiv，以及将加法和减法运算符合并为一个终结符addsub。每一次这样的替换都会移除一个终结符符号和一个产生式。这三项改动产生了如图3.34(a)所示的简化表达式语法。
   • 该语法生成了一个更小的冲突集（CC），从表中删除了行。因为语法拥有的终结符符号较少，所以表的列也较少。
   • 由此产生的Action和Goto。Action表包含132个条目，Goto表包含66个条目，总计198个条目。与原始语法的表及其384个条目相比，这样做非常有利。改变语法使得表大小减少了48%。

2. 合并行或列

   • 将相同的行或列合并是一种优化技术，它可以通过消除冗余来进一步减小解析表的尺寸。当某些状态在Action表中对所有输入符号有着完全相同的动作时，这些状态的行就可以合并为一行。同样地，如果Goto表中有若干状态对于非终结符有着相同的转移状态，那么这些列也可以合并。这种合并不仅减少了表的空间占用，还可能简化了解析过程。通过这种方式，即使在已经经过初步优化的表中，也有可能实现额外的效率提升。
   • 合并行和列的机制类似于上一节讨论的用于缩减DFA转换函数表的技术。这些技术直接减少了表的大小。如果这种空间缩减为每次表访问添加了额外的间接层，则必须直接权衡这些内存操作的成本与内存节省。表生成器也可以使用其他技术来表示稀疏矩阵——同样，实现者必须考虑内存大小与任何访问成本增加之间的权衡。

3. 直接编码表

   • 每个状态变成一个小的case语句或一系列if-then-else语句，用于测试下一个符号的类型并执行移进、归约、接受或报告错误等操作。Action和Goto表被代码所取代。
   • 由此产生的解析器避免了直接表示Action和Goto表中的所有“不关心”状态，这些在图表中显示为空白。这种空间节省可能会因为代码量增大而被抵消，因为现在每个状态都需要代码。然而，新的解析器没有解析表，不执行表查找，并且缺少骨架解析器中的外部循环。尽管其结构使得人类几乎无法阅读，但它的执行速度应该比对应的基于表的解析器更快。使用适当的代码布局技术，所产生的解析器可以在缓存和虚拟内存中表现出强大的局部性。例如，编译器编写者应将表达式语法的例程放在虚拟内存中的单一页上，以便它们不会在代码缓存中相互冲突。

使用其他构造方法

存在几种其他的用于构造LR风格解析器的算法。这些技术中包括简单的LR(1)构造，即SLR(1)，以及具有向前查找功能的LR(1)构造，即LALR(1)。这两种构造方法产生的表都比规范的LR(1)算法要小。

SLR(1)算法接受的语法类别比规范的LR(1)构造要少。SLR(1)语法受到限制，使得填表算法能够通过FOLLOW集合区分移进条目和归约条目。这一限制消除了项目中对向前查找符号的需求。结果是规范项目集的集合状态更少，因此表的行数也更少。此技术接受了众多具有实际兴趣的语法。

LALR(1)算法依赖于这样的观察：代表一个状态的集合中的核心项目是关键的，并且剩余的项目可以通过计算其闭包来添加到集合中。LALR(1)表构造使用核心项目来计算规范集合，并在达到固定点后计算它们的闭包。它产生了一个与SLR(1)构造所生成的大小相似的规范集合。尽管细节不同，但表的大小相似。

本章前面介绍的规范LR(1)构造是这些表构造算法中最通用的。它生成的表最大，但接受的语法类别也是最广的。通过适当的表简化技术，LR(1)表可以接近那些由较为有限的技术所产生的表的大小。

SLR(1)构造接受的语法类别比LALR(1)构造要少。反过来，LALR(1)构造接受的语法类别又比规范的LR(1)构造要少。然而，在一个稍微反直觉的结果中，任何拥有LR(1)语法的语言也同时拥有SLR(1)和LALR(1)语法。这些更为严格的构造算法的语法必须以某种方式成形，以便算法能够区分移进动作和归约动作。

更新日志

2025/1/14 14:30

查看所有更新日志

• c7425-更新中间代码生成于 2025/1/14