首先从矩阵最朴素的乘法开始写

假设有要计算矩阵 $C=A*B$,其中 $A \in \mathbb{R}^{M*K},B\in \mathbb{R}^{K*N}$。那么 $C \in \mathbb{R}^{M*N}$ 。那么使用C++,可以写出最朴素的矩阵乘法。使用A的 $i$行乘以B的 $j$列,通过遍历内部循环 $K$,得到 $C[i][j]$的值

void matirixSerial(float* A,float* B,float* C,int M,int K,int N){
  for(int i=0;i<M;i++){
    for(int j=0;j<N;j++){
      float temp=0;
      for(int s=0;s<K;s++){
        temp+=A[i*K+s]*B[s*N+j];
      }
      C[i*N+j]=temp;
    }
  }
}

Nvidia CUDA 简单并行化矩阵乘法

如果有GPU的前置知识的话这个也很容易理解并写出来,后面应该会更新简单说一说GPU的编程模型。上文的乘法,则是一个CPU核心计算了所有工作。为了加速计算,我们希望通过多线程的方式来进行加速,即SIMT(Single Instruction Multiple Thread)单指令多线程。在这里,就一句话来说,将任务分为多个线程,给CUDA Core去执行。

__global__ void matrixKernel(float *dA, float *dB, float *dC, int M, int K, int N){
  // 获取线程的唯一ID
  int row = blockIdx.y * blockDim.y + threadIdx.y;
  int col = blockIdx.x * blockDim.x + threadIdx.x;
  if(row < M && col <N){
    float sum1=0.0f;
    for(int s=0;s<K;s++){
      sum1+=dA[row*K+s]*dB[s*N+col];
    }
    dC[row*N+col]=sum1;
  }
}

下面简单解释下代码,假设 $A,B,c$的数据已经读到了全局内存中。根据Nvidia GPU的编程模型,有两个关键数据来决定任务的划分,即blockDim和gridDim。这个两个数据类型都Dim3的,也就是三维的。想象一下,有一个 $100*10*10$ 的立方体,这个对应着整个grid。这个立方体被切分成 $10$ 个 $10*10*10$的小立方体.那么gridDim =(10,1,1),而blockDim =(10,10,10)。并且规定立方体的不可被分割的最小尺寸为 $1*1*1$。这个最小尺寸的立方体就对应着一个CUDA Core。对于矩阵的乘法,应该实际上采用二维来处理,简单的对应就是一个CUDA Core 对应 $C$ 中的一个要计算的值。所以通过上述代码中计算的row 和 col,分别对应要计算的 $C[i][j]$,再对应到相应的 $A$ 的 $i$ 行乘以 $B$ 的 $j$ 列。

Nvidia CUDA 共享内存优化矩阵乘法

那么上面的代码存在的问题是什么呢,就是每次计算 $C[i][j]$ 的时候,都需要把 $A$ 的 $i$ 行和 $B$ 的 $j$ 列从全局内存中重新读进来一次,实际在矩阵乘法中,并不需要你每次都重新读内存。因为 $A$ 的 $i$ 行都可以用来计算 $C[i]$ 行上的数据。同理可以应用到 $B$ 的分析上去。 知道上面的问题,就可以采取更进一步的优化了,采取共享内存的优化,在Nvidia GPU中的内存模型,存在一种共享内存,被一个block内的线程共享,可以先把数据读进共享内存,再统一进行计算,达到加速计算的结果。共享内存可以理解为全局内存的缓存,也就是更底层一步的缓存,所以塌的访问速度要大于全局内存的访问速度。下面给出代码。

#define TILE_WIDTH =32 
__global__ void matrixKernel(float *dA, float *dB, float *dC, int M, int K, int N){
  __shared__ float sa[TILE_WIDTH][TILE_WIDTH];
  __shared__ float sb[TILE_WIDTH][TILE_WIDTH];
    // 获取线程的唯一ID
  int row = blockIdx.y * blockDim.y + threadIdx.y;
  int col = blockIdx.x * blockDim.x + threadIdx.x;
    
    // 初始化输出值
  float sum = 0.0f;
    //分段共享读取 
    // 计算每个线程块需要迭代的次数
  int numTiles = (K + TILE_WIDTH - 1) / TILE_WIDTH;
  for(int t=0;t<numTiles;t++){
    if(row < M && t*TILE_WIDTH+threadIdx.x < K){
      sa[threadIdx.y][threadIdx.x]=dA[row*K+t*TILE_WIDTH+threadIdx.x];
    }else{
      sa[threadIdx.y][threadIdx.x]=0.0f;
    }

    if(col < N && t*TILE_WIDTH+threadIdx.y < K){
      sb[threadIdx.y][threadIdx.x]=dB[(t*TILE_WIDTH+threadIdx.y)*N+col];
    }else{
      sb[threadIdx.y][threadIdx.x]=0.0f;
    }
    __syncthreads(); 
    // 计算部分积
    for (int k = 0; k < TILE_WIDTH; ++k) {
      sum += sa[threadIdx.y][k] * sb[k][threadIdx.x];
    }
    __syncthreads(); 
	}

  // 将结果写回全局内存
  if (row < M && col < N)
    dC[row * N + col] = sum;
}

代码中已经进一步优化了计算,以防止数组太大的情况下,$A$ 和 $B$ 的数据不能一次性读到共享内存里,所以进行了分块。

重要

其中代码 26行和31行处的__syncthreads();其中26行的是为了同步,因为多线程,无法确保计算的顺序,我们使用共享内存是为了提高内存利用率,也就是不止一个线程来使用共享内存,所以应该等待所有的线程都完成了共享内存读取,才能利用共享内存进行计算。第31行的目的,是为了位于内部循环,也就是在每个线程块中的线程已经完成了当前分段(tile)上的部分积计算之后。这个同步点的作用是确保所有线程都完成了当前分段上的乘法累加操作,这样在进行下一个分段的数据加载时,不会出现数据覆盖或使用旧数据的情况。

提示

因为上面说了共享内存其实也就是被一个block里的线程所共享,所以我们可以把共享内存的大小设为blockDim对应的大小,那么如何实现这一点呢。我们可以使用模板来实现。下面仅给出函数签名

template <int BLOCK_DIMx,int BLOCK_DIMy>
__global__ void matrixKernel(float *dA, float *dB, float *dC, int M, int K, int N)

Nvidia CUDA 共享内存优化矩阵乘法V2

上面使用共享内存优化依然存在的问题是,我们还是用一个线程去对应一个值的计算,我们应该使用一个线程对多个值的计算。针对上面的内存优化,我们采取下面的假设,一个线程块处理 $TM*TN$ 的数据,而一个block处理 $BM*BN$ 的数据。
那么就有 $BM={BLOCK\_DIMx}*TM,BN={BLOCK\_DIMy}*TN$。$BK$则为内部循环K上面的分块。目的同样是为了避免溢出共享内存。下面给出代码。

template <int BM, int BN, int BK, int TM, int TN>
__global__ void matrixKernel(float *dA, float *dB, float *dC, int M, int K, int N){
  __shared__ float SA[BM * BK];
  __shared__ float SB[BK * BN];
  int curCol = TM * (threadIdx.x + blockIdx.x * blockDim.x);
    //curCol代表处理到哪一列
    //curRow代表处理到哪一行
  int curRow= TN * (threadIdx.y + blockIdx.y * blockDim.y);
  int numTiles = (K + BK - 1) / BK;
  float tmp[TM * TN] = {0.0f};
    //一个线程块block计算BM*BN,每个线程计算C中的TM*TN
    //BM=BLOCK_DIM_x×TM,BN=BLOCK_DIM_y×TN
  for(int t=0;t<numTiles;t++){
    //先读取SA
    for(int indexa=0; indexa < TM; indexa++){
      for(int indexk=0;indexk <BK;indexk++){
        if(curRow+ indexa < M && indexk + t*BK <K){
          SA[(threadIdx.x * TM + indexa) * BK + indexk] = da[(curRow+indexa)*K+indexk+t*BK];
        }else{
          SA[(threadIdx.x * TM + indexa) * BK + indexk] = 0;
        }
      }
    }
    __syncthreads();

    for(int indexb = 0;indexb <TN;indexb++){
      for(int indexk=0;indexk<BK;indexk++){
        if(curCol + indexb <N && indexk+t*BK<K){
          SB[indexk*BN + threadIdx.y*TN +indexb ] = dB[(indexk+t*BK)*N+curCol+indexb];
        }else{
          SB[indexk*BN + threadIdx.y*TN +indexb] = 0;
        }
      }
    }
    __syncthreads();

    for(int indexm=0;indexm < TM;indexm++){
      for(int indexn =0;indexn <TN;indexn++){
        for(int indexk=0;indexk<BK;indexk++){
          tmp[indexm*TN+indexn] += SA[(threadIdx.X*TM+indexm)+indexk]*SB[indexk*BN+threadIdx.y*TN+indexn];
        }
      }
    }
    __syncthreads();
  }

  for(int indexm =0;indexm <TM;indexm++){
    for(int indexn=0;indexn <TN;indexn++){
      if(curCol+indexm < M && curRow+indexn <N){
        dC[(curCol+indexm)*N+curRow+indexn] = tmp[indexm*TN+indexn];
      }
    }
  }
}

上面的代码,一个线程处理了多个元素,并且使用的共享内存,计算的效率进一步提升。 以上的最基本的Gemm的优化,下面的优化,需要使用更多的技巧,和更多的GPU编程知识。

Nvidia CUDA 共享内存优化矩阵乘法V3

这一步优化,主要针对特定长度的矩阵,优化从全局内存加载到共享内存的过程。假如在上述矩阵中 $M=N=K=1024$。那么我们可以选择 $blockDim=(32,32,1),TM = TN =4,BK=8$; 那么 $SA \in \mathbb{R}^{128*8},SB\in \mathbb{R}^{8*128}$,计算得到 $\mathbb{R}^{128*128}$ 的子矩阵。
$0<=tid=threadIdx.x + threadId.y*blockDim.x <=1023$
$\mathrm{smem\_a\_m=tid \% 2 \in\{0,..., 127 \}, smem\_a\_a=tid / 2 \in\{0,...,8 \}}$
$\mathrm{smem\_b\_k=tid \% 32 \in\{0,..., 8 \}, smem\_a\_a=tid / 32 \in\{0,...,127 \}}$
这种做法的特点是: $BM*BK=BN*BK=BLOCK\_DIMx*BLOCK\_DIMy$,需要重新根据一维线程索引排布为二维索引,并且保证SA和SB的大小正好和线程块的线程数目一致。 下面给出代码。

/*
const int TM = 4;
const int TN = 4;
const int BLOCK_DIM_x = 32;
const int BLOCK_DIM_y = 32;
const int BM = TM * BLOCK_DIM_x;
const int BN = TN * BLOCK_DIM_y;
const int BK = 8;
*/
template <int BM, int BN, int BK, int TM, int TN>
__global__ void matrixKernel(float *dA, float *dB, float *dC, int M, int K, int N)
{
    // blockDIM=(32,32,1),TM=TN=4,BK=8,1024*1024的乘法
  __shared__ float SA[BM * BK];
  __shared__ float SB[BK * BN];
  int curCol = TM * (blockIdx.x * blockDim.x);
  int curRow = TN * (blockIdx.y * blockDim.y);
    //SA形状为[128,8],SB形状为[8,128],计算得到形状为[128,128]的子矩阵
  int width = (K + BK - 1) / BK;
  float tmp[TM * TN] = {0.0f};
  int tid = threadIdx.x + threadIdx.y * blockDim.x;
    //线程重排
  int smem_a_m = tid % 2;//分块内部行号
  int smem_a_k = tid / 2;//分块内部列号
  int smem_b_k = tid % 32;//分块内部行号
  int smem_b_n = tid / 32;//分块内部列号
  for (int ph = 0; ph < width; ph++)
  {
    (float4 &)SA[smem_a_m * BK + 4 * smem_a_k] = (float4 &)dA[(curCol + smem_a_m) * K + 4 * smem_a_k + ph * BK];
    (float4 &)SB[smem_b_k * BN + 4 * smem_b_n] = (float4 &)dB[(smem_b_k + ph * BK) * N + curRow + 4 * smem_b_n];
    for (int id = 0; id < 4; id++)
    {
      if (curCol + smem_a_m >= M || ph * BK + 4 * smem_a_k + id >= K)
      {
        SA[smem_a_m * BK + 4 * smem_a_k + id] = 0.0f;
      }
      if (curRow + 4 * smem_b_n + id >= N || smem_b_k + ph * BK >= K)
      {
        SB[smem_b_k * BN + 4 * smem_b_n + id] = 0.0f;
      }
    }
    __syncthreads();
    for (int index_q = 0; index_q < TM; index_q++)
    {
      for (int index_v = 0; index_v < TN; index_v++)
        {
          int reg_c_m = threadIdx.y * TM + index_q;
          int reg_c_n = threadIdx.x * TN + index_v;
          for (int index_k = 0; index_k < BK; index_k++)
          {
            tmp[index_q * TN + index_v] += SA[reg_c_m * BK + index_k] * SB[index_k * BN + reg_c_n];
          }
        }
    	}
      __syncthreads();
    }
    for (int index_q = 0; index_q < TM; index_q++)
    {
      for (int index_v = 0; index_v < TN; index_v++)
      {
        int reg_c_m = threadIdx.y * TM + index_q;
        int reg_c_n = threadIdx.x * TN + index_v;
        if (curRow + index_q < M && curRow + index_v < N)
        {
          dC[(curRow + reg_c_m) * N + curRow + reg_c_n] = tmp[index_q * TN + index_v];
        }
      }
    }
}

下面给出图示大致意思

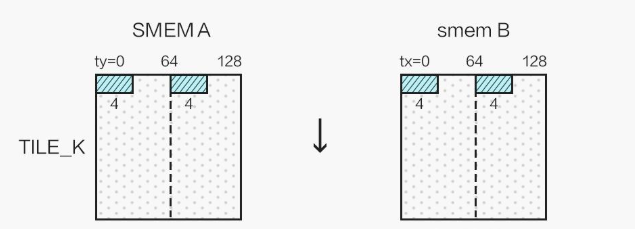
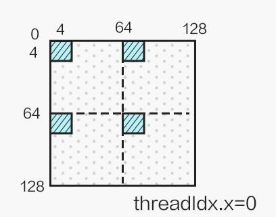
实际上上图对SA还做了一次转置来避免bank conflict,在下一节中补充。与此相关的还有float4优化,也是只能针对特定长度的数组来进行优化。

第二重量级的优化,避免bank conflict

什么是Bank。Shared Memory 为了提高带宽,划分成了不同的 bank,bank 之间可以并行访问。比较新的 GPU 有 32 个 bank,每个 bank 的宽度是 4 Bytes。Shared Memory 地址和 bank 的关系如下图所示,bank = (Byte-Address / 4) % 32.

bank示意图

• 什么是 bank conflict ? 同一个 warp 内的多个线程(>=2)访问了同一个 bank 内的不同地址的 4B word (可以理解为 bank 内的不同"行"),这些访存请求将会串行
• 不同 warp 之间的线程不会发生 bank conflict
• 如果多个线程访问了同一个4B word(或者同一个 4B word 内的 bytes),不会发生 bank conflict,而是会 broadcast
• 示例：
  • 下图中,每个线程访问不同的 bank,不会发生 bank conflict

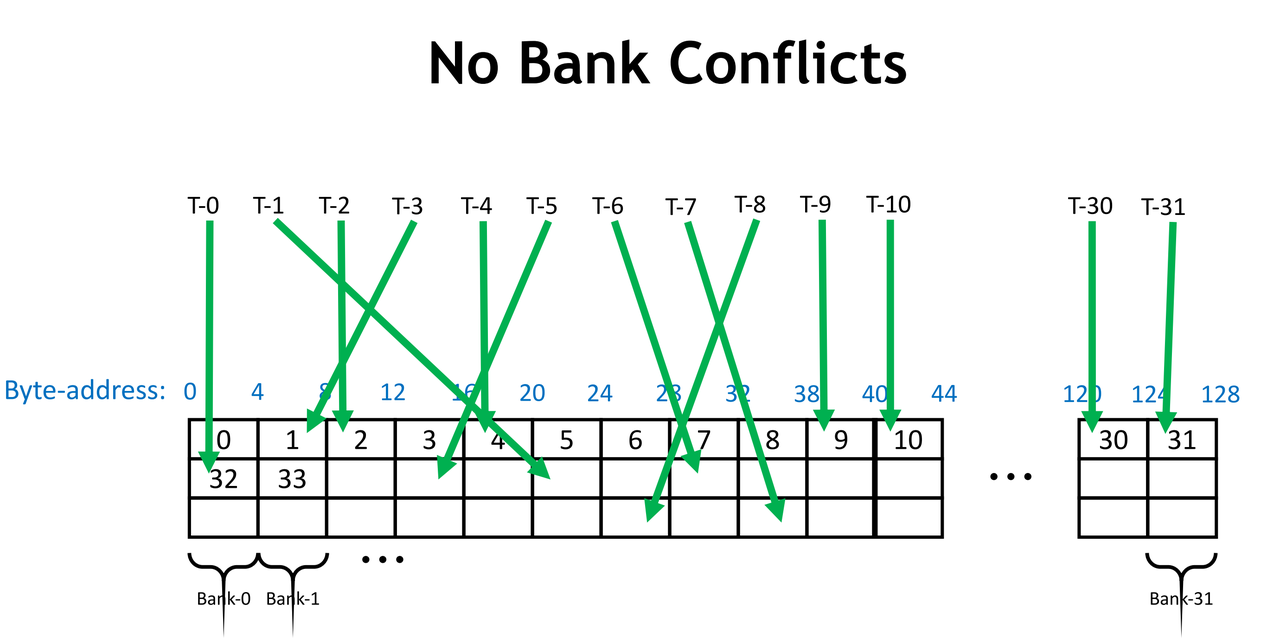
• 下图中,T-0 和 T-1 访问了 bank 1 中的 word 1 和 word 33,发生 bank conflicts。因为不同的 word 数有两个,所以是 2-way bank conflict

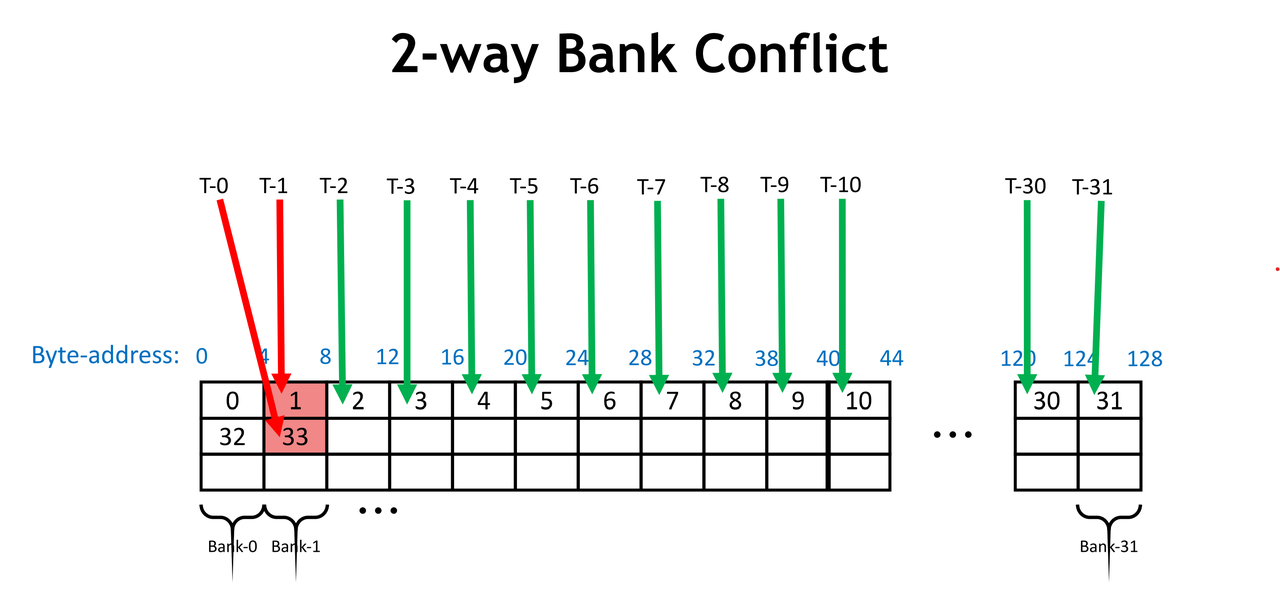
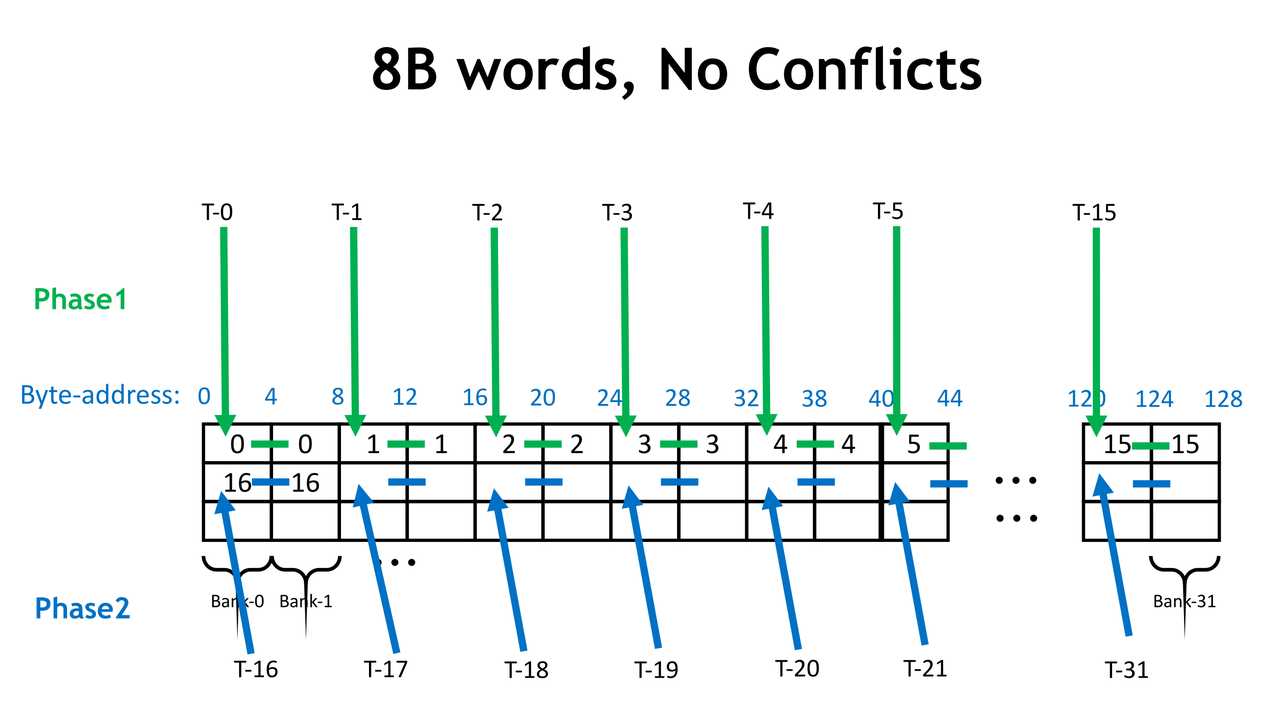
• Bank Conflict Resolution 如果每个线程访问的 Bytes 数比较大,比如每次访问 8B,那么 warp 中32个线程访问连续的地址时,一定会出现 bank conflict。GPU 对这种情况有一些 resolution 机制resolution

通过这个 resolution,可以认为 bank 的数量和宽度和线程访问的大小相关。当线程访问 8B words 时,相当于只有 16个宽 8B 的 bank,16B 的情况同理。下面的情况认为没有 bank conflict

讲完了banK的基本知识,那么来进行优化,只要对SA的load进行一个转置就可以了。这一点会在下一个章节Cutlas实现Gemm中有详细说明。

最具重量级的优化Cutlas源码实现

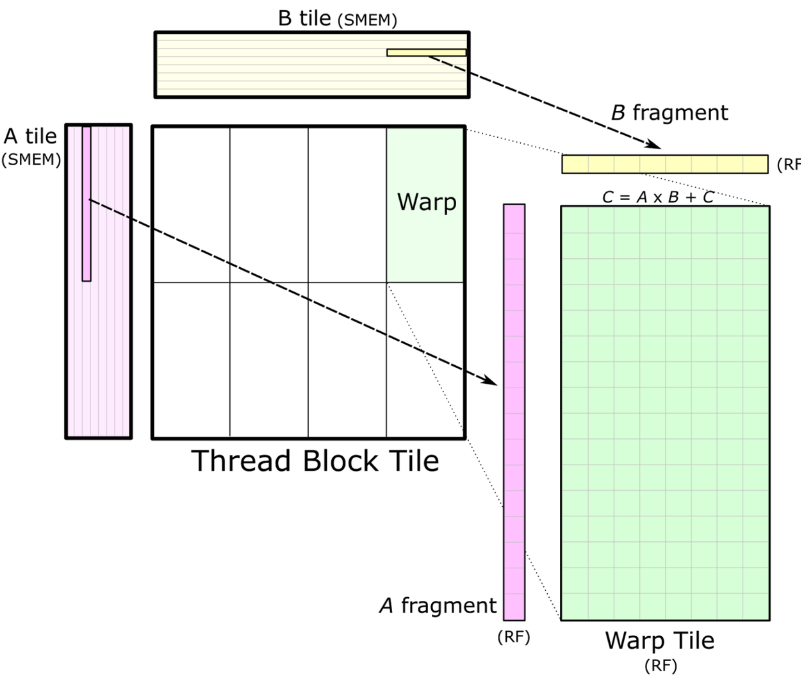
• 把 GEMM 转化为外积计算，输出的 M x N 分成 tile，各 tile 之间的计算是互不影响的，可以并行。为每一个 tile 分配一个 threadblock 计算
• 因为直接访问显存 （Global Memory）latency 很高，并且每个数据都会重复使用。所以把数据先搬运到更高速的存储上，再继续处理
• 输入矩阵因为要做频繁的累加计算，放在最快的寄存器（Register File）上
  • Register File 是对每个线程私有的
• A，B 矩阵的数据因为需要被各线程共享，放到 Shared Memory 上

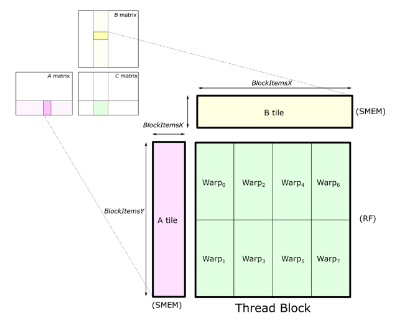
A,B 矩阵一般一次只加载一部分到SMEM(限于SMEM size),这里在 K 维上有个循环,是 GEMM 的主循环。主循环内加载数据和计算可以 overlap,形成一个 pipeline,用计算掩盖数据访问的耗时。如下图所示：

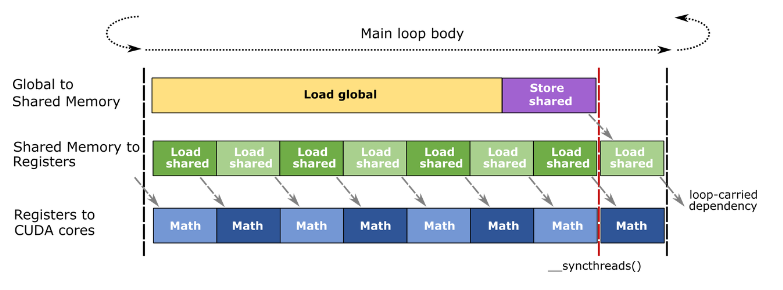
• 大致流程：
  1. 主循环的一轮开始前,load from Global Memory,调用一次 _syncthreads(),保证 shared memory 是加载好的
  2. 主循环中,对 warp tile 也在 k 维上有一个循环(内层循环),在内层循环每一轮中 load from Shared Memory 和调用 warp-level mma 是 overlap 的
• _syncthreads() 是一个 barrier,当同一个 threadblock (不是 warp)中的所有 thread 都达到_syncthreads() 的位置时,才会继续执行
• 从 Shared Memory 读取数据到 Register File,再继续进行计算

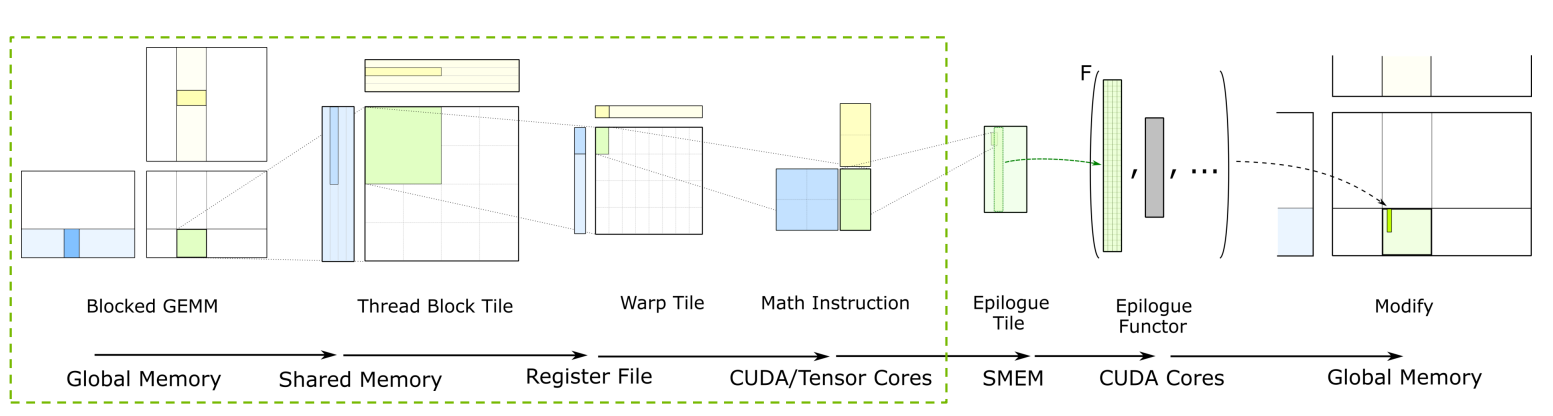
• 从 Shared Memory 读取数据到 Register File，再继续进行计算

Cutlass 如何解决 bank conflicts

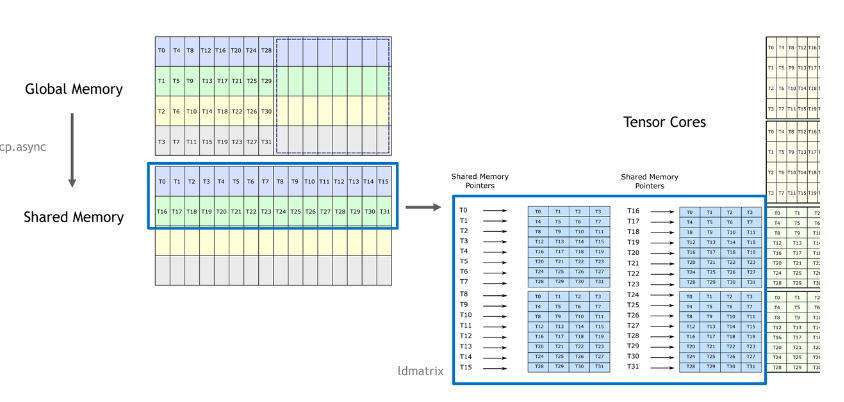
• 上图中,A矩阵从 Global Memory 加载到 Shared Memory,然后调用 ldmatrix 指令加载到 Register File,最后用 Tensor Core 指令计算
• 每个方块(每个线程)对应 128 bit 数据,所以 warp 中线程分为 4 个 phase 执行访存,Shared Memory 共有 8 个 128 bit 的 bank
• A矩阵是 Column Major,因此在从 Global Memory 中读取时,每个 phase 读两列,写到 Shared Memory 也是写前两列
• 线程中 SMEM 指针和目标寄存器的排列如上图右侧所示。

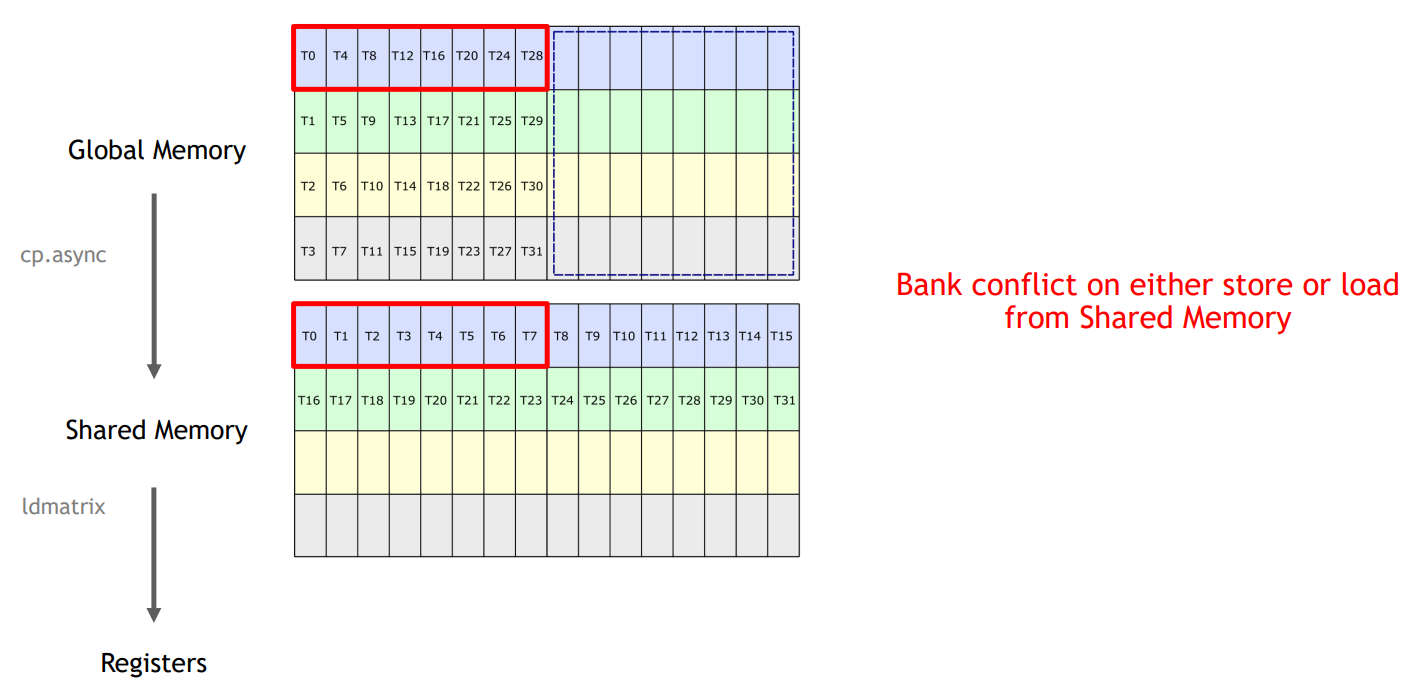
• 上面是英伟达GTC大会PPT上的截图。至于图中的Shared Memory 的读和写一定有一个会 bank conflict。
  自己想的还不是特别明白。
• 参考Cutlass链接
• 大概的意思就是，为了后续从share memory 到 register的load过程避免bank conflict
• 解决方法
  • 按照下面的方式重排,Shared Memory 为 Row Major
    • Store 时,一个 phase 内的线程写入到一行,因为是 Row Major,不会 bank conflict
    • Load 时,相同颜色的方块,在 tile 中的逻辑位置是一行,ldmatrix 读取时,逻辑上还是读取前两行,但是物理位置上,可以看到在一个warp内,每个颜色的方块在每一列(对应一个bank)都只有一个,所以也是没有 bank conflict 的

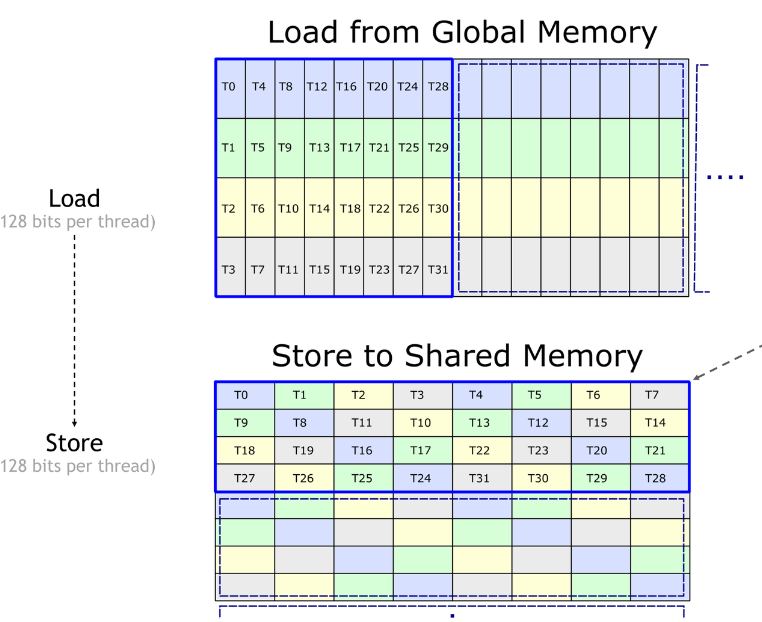
在图中，一个 warp 范围的内存访问以蓝色突出显示，单个线程加载一个 128 位向量。全局内存中的 tile 可以对应于 activations 或 filters，并假设是 “strip-mineed” 的，有四个线程加载连续的通道。
共享内存可视化为“行优先”矩阵，其中八列表示 八个 128 位 SoundBank 的调用。如果每个 WARP 满足以下条件，则对共享内存的访问将是无冲突的：

• {T0， T1， ..， T7} 不访问同一个 128 位bank
• {T8， T9， ..， T15} 不访问同一个 128 位bank
• {T16， T17， ..， T23} 不要访问同一个 128 位bank
• {T24， T25， ..， T31} 不访问同一个 128 位bank
  为了实现无冲突存储，Shared Memory 布局重新映射了 strip-mineed 排列以转置向量，并对每个线程指针的列索引应用 XOR 操作。具体说来

  int store_column = (lane_id % 8) ^ (lane_id / 8);

布局上的这种转换将有助于从共享内存读取数据切片，以使用 Tensor Core 计算 warp 级矩阵乘法。

下一步是从share memory 到 register的load过程避免bank conflict

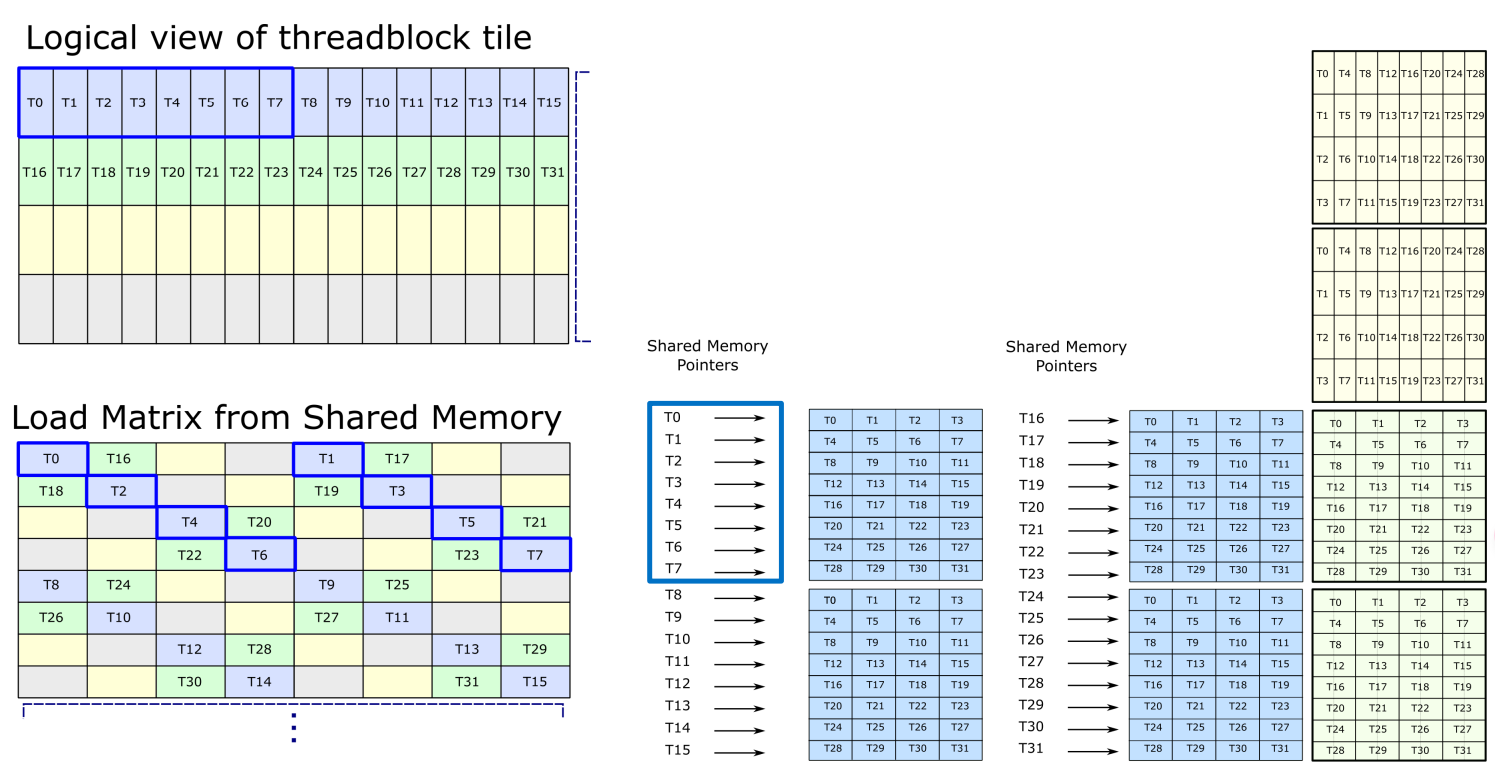
上图显示了参与 ldmatrix 指令的前 8 个线程如何在逻辑上映射到共享内存中矩阵的 C=0..31 切片。此切片在代码中称为 “k-group”，因为它对应于 warp 级矩阵乘法的相同 K-index。
例如，为了加载上图右侧的矩阵，LDMATRIX 会在“线程块平铺的逻辑视图”中加载前 8 个 128b 向量，标记为 T0-T7。这些对应于“从全局/存储加载到共享”图中的 T0、T4、T8、T12、T16、T20、T24、T28。如果没有排列布局，T0、T8、T16、T24 都将位于列/组 0 中，而 T4、T12、T20、T28 都将位于列 4 中。
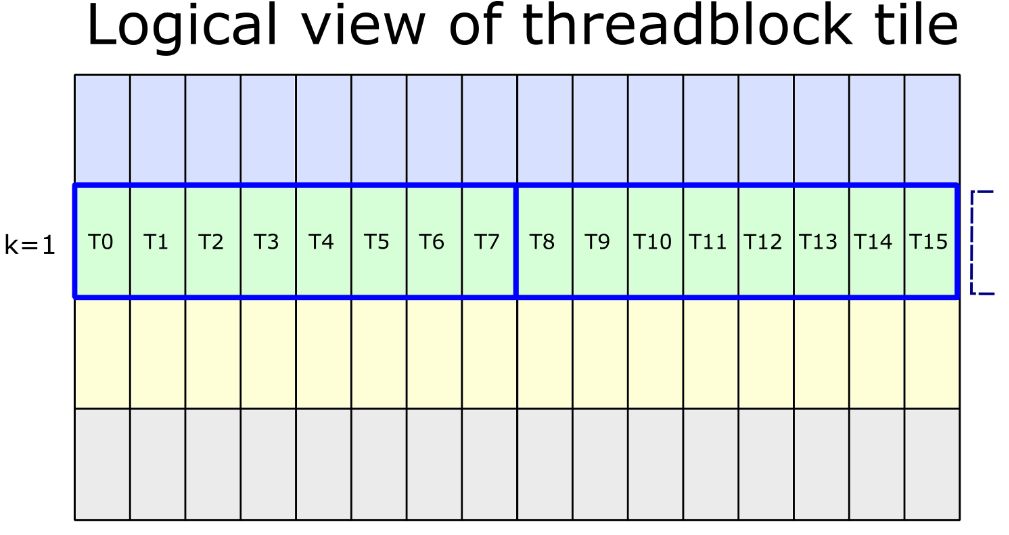
要前进到共享内存中的下一个 “k-group”，请按照以下顺序使用 XOR 操作更新指针。

• ^1 从 k=0 前进到 k=1
• ^3 从 k=1 到 k=2
• ^1 从 k=2 前进到 k=3
• ^3 从 k=3 前进到 k=0

这些过渡中的第一个如下所示

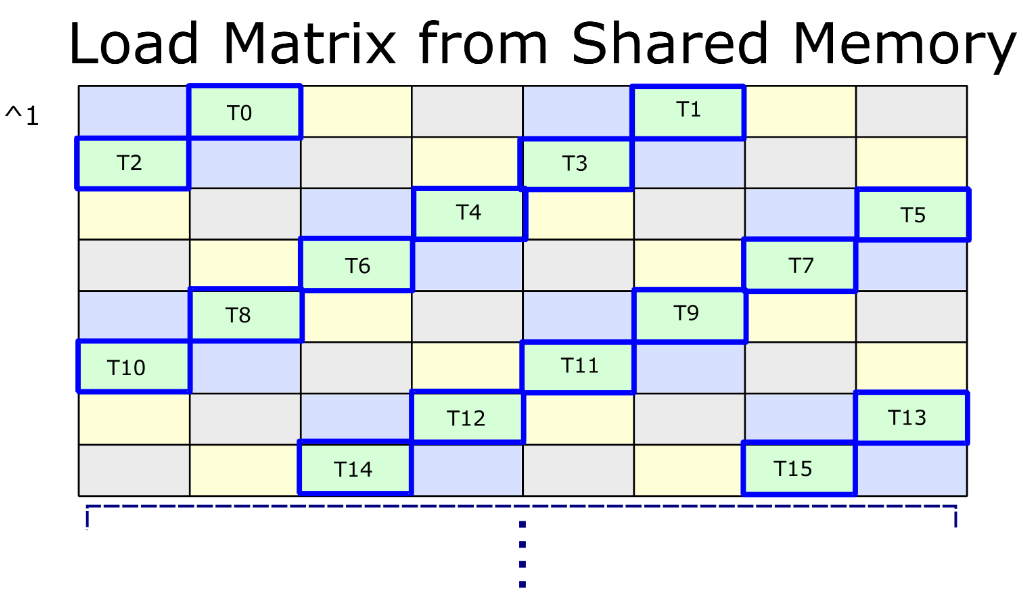
至此先告一段落,期待后续更新优化 2024.12.3

更新日志

2024/12/3 07:12

查看所有更新日志

• 9985d-fix the fault add avateir add leetcode于 2024/12/3